[차한잔] 읔... 복소수 답변 달고 있었는데 삭제되었네요.
2
1748
2021-01-26 02:54:56
글 쓰신 분이 사정이 있으셔서 삭제하셨겠지만,
답 다는 도중에 삭제되니 허탈하네요 ㅠㅠ
암튼... 근호의 분리는 0보다 작을 때는 안되요 ㅠㅠ
12
Comments
| 글쓰기 |




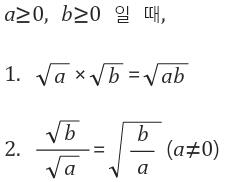



그러게요.
그리고 그렇게 표시 하시면 복소수가 아닌거구요. 그냥 루트죠 제곱근 구하는
플러스 마이너스 3일뿐이죠.
허수. 복소수 개념부터 잡으셔야 할듯 합니다.